Da un’idea di Rosaria Pedri

Scuola Primaria di Piazza al Serchio (Lu)

Superare l’astrazione della matematica

L’insegnamento di concetti matematici astratti, come quello di frazione, rappresenta una delle sfide più complesse nella scuola primaria. La difficoltà per gli alunni di connettere simboli e procedure a un significato concreto può generare disaffezione e ostacolare un apprendimentoApprendimento 'Il SNC non sarebbe in grado di sviluppare in modo autonomo, solo sulla spinta offerta dal DNA, tutte le sue potenzialità di pensiero e di linguaggio, come talora dà l'impressione di fare e come spesso viene erroneamente ritenuto. Sarà invece compito di ogni bambino attivare all'interno del proprio SNC queste potenzialità, con la costruzione di circuiti fra neuroni e ulteriori circuiti fra circuiti gi? formati, finendo anche col modificare intensamente dal punto di vista funzionale tutta la struttura nervosa disponibile. Questo attivo processo di costruzione si identifica con l'apprendimento. Apprendimento che ha luogo continuamente e intensamente soprattutto nei primi anni, durante ogni momento di veglia. Sostituire il concetto di sviluppo con il concetto di costruzione non è soltanto un gioco di parole, ma un modo di orientare in forma completamente diversa l'ottica e il compito dell'educazione e dell'insegnamento. Infatti, mentre l'idea di sviluppo si ricollega alla graduale comparsa di qualcosa che è predestinata già fino dal concepimento, l'idea di costruzione comporta la riconsiderazione e la valorizzazione dell'opera degli educatori e di tutto il contesto ambientale che circonda il piccolo. ', 4578 profondo e duraturo. Per superare questo scoglio, la didattica contemporanea si affida sempre più a metodologie che pongono lo studente al centro del processo di apprendimento, trasformando l’aula in un laboratorio di scoperta. L’approccio costruttivista e laboratoriale, in particolare, si rivela uno strumento potente per rendere la matematica un’esperienza tangibile e significativa.

Questo articolo si propone di analizzare l’efficacia di tale approccio attraverso l’esame di un percorso didattico specifico, “Frazioni in Gioco”, realizzato in una classe terza della scuola primaria di Piazza al Serchio. Partendo da un solido quadro pedagogico, descriveremo in dettaglio le fasi operative che hanno guidato gli alunni dalla manipolazione di semplici tovagliette alla comprensione delle operazioni con le frazioni. Valuteremo infine i risultati ottenuti, non solo in termini di apprendimento disciplinare per gli studenti, ma anche di crescita professionale per i docenti, per trarre delle riflessioni conclusive sulla validità e trasferibilità del modello.

1. Il quadro pedagogico di riferimento

Ogni percorso didattico efficace poggia su un solido quadro teorico che ne garantisce la coerenza interna e l’intenzionalità educativa. La pratica in aula non può essere una sequenza estemporanea di attività, ma deve discendere da principi pedagogici chiari che orientano le scelte metodologiche, la selezione dei contenuti e le modalità di valutazione. Il progetto “Frazioni in Gioco” si fonda su un’impalcatura teorica robusta e stratificata.

I fondamenti del percorso affondano le radici nell’approccio costruttivista, che concepisce l’apprendimento non come una trasmissione passiva di nozioni, ma come un processo attivo in cui lo studente costruisce la propria conoscenza a partire da esperienze concrete e condivise. Questa visione è stata declinata seguendo l’ispirazione metodologica della Dott.ssa Baccaglini Frank e integrata con i principi del metodo Galileo for Education, che da oltre un decennio costituisce il riferimento pedagogico dell’istituto. Il percorso è stato inoltre monitorato da un’équipe di esperti, tra cui il Prof. G. Giuntoli, la Dott.ssa J. Bickel, a garanzia del rigore metodologico. Questo framework costruttivista necessita di un superamento della didattica astratta basata su esercizi ripetitivi, esigendo invece un innesco per l’apprendimento radicato in un contesto significativo: un ruolo qui adempiuto dal “compito autentico” del pizzaiolo.

Tale impostazione teorica assicura piena coerenza con gli obiettivi formativi istituzionali, delineati dalle Indicazioni Nazionali e dal Curricolo d’istituto. Le attività proposte sono state progettate per sviluppare non solo conoscenze disciplinari, ma anche un insieme di competenze chiave, tra cui:

• Comprensione del concetto di frazione come parte di un intero, attraverso modelli concreti, disegni e simboli.
• Capacità di argomentare e comunicare i procedimenti seguiti, giustificando le proprie scelte.
• Utilizzo di strumenti e materiali manipolativi per esplorare, rappresentare e risolvere situazioni problematiche.
• Collaborazione attiva nelle attività di gruppo, contribuendo in modo responsabile al lavoro comune.
• Sviluppo di competenze metacognitive, come la capacità di riflettere sui propri errori e di utilizzarli come occasione di apprendimento.

Questa solida impalcatura teorica e istituzionale ha permesso di trasformare i principi pedagogici in un’azione didattica concreta e mirata, di cui ora analizzeremo la struttura e l’implementazione.

2. Metodologia e struttura del percorso didattico: il compito autentico come motore dell’apprendimento

La logica della didattica laboratoriale trasforma l’aula da luogo di ascolto a spazio di scoperta, sperimentazione e costruzione condivisa del sapere, utilizzando materiali semplici e facilmente reperibili come fogli, cartoncini, piatti di carta e cubetti. In questo paradigma, il motore che innesca il processo di apprendimento è un compito significativo, capace di catturare l’interesse degli alunni e di dare un senso al loro impegno.

L’elemento catalizzatore del percorso è stato il “compito autentico” proposto dal “pizzaiolo Nino Terzini“, una figura narrativa che ha lanciato una sfida concreta e motivante alla classe:

“Ciao bambini, sono il pizzaiolo Nino e avrei bisogno del vostro aiuto. […] Vorrei che le tovagliette fossero composte da diverse parti colorate […] Ognuna di queste parti deve essere ricavata dividendo la tovaglietta in parti rigorosamente della stessa grandezza.”

Questo approccio narrativo si è rivelato estremamente efficace: ha collegato un concetto astratto a un contesto familiare e stimolante; Il percorso si è quindi articolato in una sequenza logica di fasi, costruite per guidare gli alunni da un’esplorazione intuitiva a una formalizzazione consapevole.

Fase 1: dall’intuizione alla scoperta concreta. Il percorso ha preso avvio con attività di manipolazione diretta: la piegatura di fogli A4 per suddividerli in due, quattro, otto parti. Questa esperienza pratica ha innescato una discussione guidata sul significato di “parti uguali”. La difficoltà aggiuntiva introdotta nella piegatura in terzi ha rappresentato un passaggio intenzionale verso un livello cognitivo più elevato, stimolando gli alunni a stimare, provare e correggere, allenando così la flessibilità cognitiva. Le risposte spontanee dei bambini, accolte e valorizzate dall’insegnante, hanno rivelato una comprensione intuitiva ma profonda del concetto.

Fase 2: la composizione delle tovagliette. Una volta create le unità frazionarie (1/2, 1/4, 1/3, 1/6, etc.), gli studenti le hanno utilizzate come “tessere” per comporre le tovagliette richieste da Nino. Lavorando su composizioni sia monocromatiche (es. solo quarti) sia policromatiche (es. mezzi, quarti e ottavi), gli alunni hanno scoperto empiricamente principi matematici fondamentali. L’attività pratica di coprire esattamente una superficie li ha portati a intuire la somma di frazioni e il concetto di intero come somma delle sue parti (es. 1/2 + 1/4 + 1/4 = 1). Domande-stimolo come “Cosa succede se usi due 1/4 e un 1/2?” o “Ci sono modi diversi per arrivare all’intero?” hanno guidato la riflessione e la verbalizzazione di queste scoperte.

Tovagliette monocromatiche

Tovagliette policromatiche

Fase 3: dalla manipolazione alla rappresentazione simbolica. Un passaggio cruciale per consolidare l’apprendimento è la transizione dall’artefatto concreto alla sua rappresentazione astratta. In questa fase, gli alunni hanno trasferito le loro tovagliette fisiche sui quaderni, disegnandole e annotando le combinazioni scoperte con il linguaggio simbolico della matematica (es. 1/3 + 1/3 + 1/3 = 1). Questo esercizio ha permesso di fissare i concetti, di costruire un ponte tra il “fare” e lo “scrivere” matematico e di iniziare a verbalizzare le prime regole operative, come “Se il denominatore è uguale, posso sommare i numeratori”.

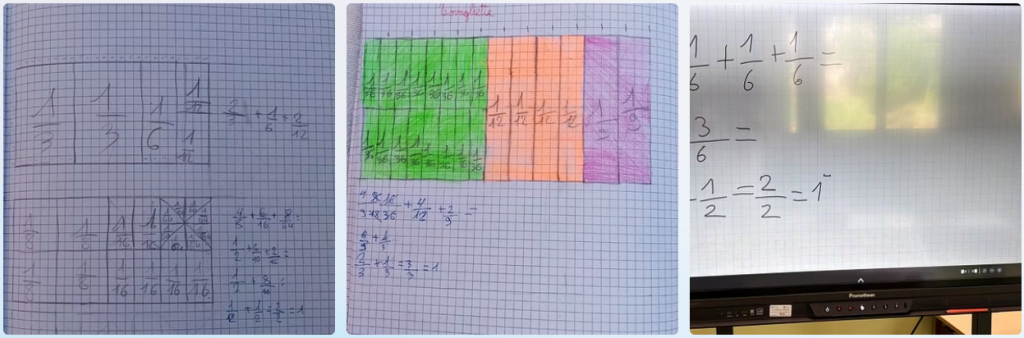
Fase 4: strategie esplorative per le operazioni. Per affrontare le operazioni con denominatori diversi, il percorso ha deliberatamente evitato l’introduzione meccanica dell’algoritmo del minimo comune multiplo. Si è privilegiato un approccio esplorativo che ha promosso una comprensione profonda attraverso una pluralità di strategie. Gli alunni hanno utilizzato supporti visivi come le strisce di carta frazionate per confrontare concretamente le lunghezze.

La tavola pitagorica è stata impiegata non come strumento mnemonico, ma come una “mappa dei multipli” per cercare visivamente denominatori comuni. Sono state inoltre proposte attività ludiche come il gioco “Trova il denominatore comodo”. Queste strategie hanno trasformato gli alunni in ricercatori attivi di soluzioni anziché in meri esecutori di procedure.

La sequenza progressiva di queste attività ha permesso di costruire un apprendimento solido e significativo, in cui ogni nuova abilità si è fondata sull’esperienza precedente, preparando il terreno a una valutazione dei risultati che va oltre la semplice verifica delle conoscenze.

3. Analisi dei risultati: un impatto a 360 gradi

L’efficacia di un percorso didattico non si misura unicamente attraverso il raggiungimento degli obiettivi disciplinari. Un intervento di qualità produce effetti positivi a tutto tondo, incidendo sullo sviluppo di competenze trasversali negli alunni, sulla loro motivazione e sul loro benessere in classe, e al contempo stimolando una crescita professionale significativa nei docenti che lo hanno progettato e condotto. L’analisi dei risultati del progetto “Frazioni in Gioco” conferma un impatto positivo su tutti questi fronti.

Benefici per gli alunni L’approccio laboratoriale ha generato una crescita tangibile negli studenti, analizzabile in tre aree distinte.

Competenze cognitive e disciplinari: L’efficacia del percorso si manifesta nel potenziamento osservato della capacità di rappresentazione, con gli alunni che passano con disinvoltura dai modelli concreti a quelli grafici e simbolici. Hanno arricchito il proprio lessico, acquisendo un linguaggio tecnico-disciplinare appropriato che ha permesso loro di verbalizzare correttamente le procedure seguite e le scoperte fatte.

Competenze trasversali e metacognitive: Si è osservato un notevole sviluppo dell’autonomia operativa e delle abilità manipolative nell’uso di strumenti e materiali. Ancora più importante, gli studenti hanno maturato una maggiore consapevolezza del proprio percorso di apprendimento, imparando a riflettere sui propri processi mentali e a riconoscere il valore dell’errore. Il lavoro di gruppo, costantemente promosso, ha inoltre potenziato le abilità sociali e relazionali, come l’ascolto e la collaborazione.

Aspetti relazionali e motivazionali: Il contesto di apprendimento, basato sulla scoperta e sulla collaborazione, ha generato un netto aumento della motivazione, dell’interesse e della partecipazione attiva. Il clima di classe, privo del timore del giudizio, ha permesso a tutti, anche agli alunni più fragili, di esprimere le proprie idee con fiducia, incrementando l’autostima e il piacere di stare a scuola.

Benefici per i docenti: il percorso non è stato solo un’esperienza formativa per gli alunni, ma ha rappresentato una preziosa occasione di crescita professionale e di riflessione sulla pratica didattica per le insegnanti, che hanno agito come veri e propri “registi dell’apprendimento”.

Riflessione sulla disciplina: la necessità di progettare attività concrete ha stimolato un approfondimento dei contenuti matematici, favorendo il confronto con esperti e la ricerca di soluzioni didattiche che andassero al cuore dei concetti.

Riflessione sulla valutazione: l’osservazione diretta dei processi di scoperta e degli errori costruttivi degli alunni ha innescato una profonda riflessione sulla valutazione, spostando il focus dalla correttezza del prodotto finale alla comprensione dei percorsi cognitivi individuali, favorendo così una valutazione più autenticamente formativa.

Riflessione sulle metodologie: l’esperienza ha consolidato una maggiore cura nella progettazione di ambienti di apprendimento inclusivi, in cui la relazione educativa diventa il perno di un insegnamento efficace e attento alle esigenze di ciascuno.

Programmazione consapevole: le docenti hanno sviluppato la capacità di una programmazione più flessibile e mirata, mettendo al centro l’apprendimento reale dei bambini e la qualità dei processi, superando la tendenza a ricercare la “perfezione formale dei prodotti” finali.

Questi risultati congiunti, che testimoniano una crescita armonica sia degli studenti sia dei docenti, confermano la validità complessiva di un approccio che investe sulla qualità dei processi tanto quanto sul raggiungimento degli obiettivi.

4. Riflessioni conclusive: il laboratorio come paradigma didattico

L’analisi del percorso didattico “Frazioni in Gioco” offre una chiara testimonianza di come un approccio costruttivista e laboratoriale possa trasformare l’apprendimento della matematica da un esercizio astratto e spesso ostico a un’avventura intellettuale concreta, motivante e accessibile a tutti. L’esperienza della classe terza di Piazza al Serchio ha dimostrato che è possibile costruire una comprensione profonda e duratura dei concetti partendo dalla curiosità degli alunni e valorizzando la loro capacità di pensare, sperimentare e collaborare.

Da questa esperienza emergono alcuni principi chiave che rendono tale approccio efficace e trasferibile ad altri contesti disciplinari:

La centralità del compito autentico e della narrazione per innescare la motivazione intrinseca e dare un senso all’apprendimento.

Il valore insostituibile della manipolazione di artefatti concreti come ponte per costruire significato e passare gradualmente all’astrazione simbolica.

Il ruolo dell’errore, non come fallimento da sanzionare, ma come tappa fondamentale e costruttiva del processo di ricerca e scoperta.

La funzione del docente come mediatore e regista dell’apprendimento, che guida la scoperta attraverso domande-stimolo senza sostituirsi al pensiero dell’alunno.

L’importanza della collaborazione tra pari e della discussione collettiva come strumenti potenti per la co-costruzione del sapere e lo sviluppo di competenze sociali.

In conclusione, la didattica laboratoriale si rivela essere molto più di una semplice “tecnica” da applicare per insegnare un argomento specifico. Essa rappresenta un vero e proprio paradigma educativo che promuove un apprendimento profondo, critico e consapevole. Educare gli studenti a costruire la conoscenza, a collaborare e a risolvere problemi reali significa dotarli degli strumenti indispensabili per un’autentica literacy matematica, fondata non sulla memorizzazione di algoritmi, ma sulla capacità di modellizzare, argomentare e risolvere problemi in modo flessibile e consapevole.